La teoría moderna de portafolios planteada por Harry Markowitz nos dice que existe una alocación óptima de los pesos de los instrumentos financieros que maximiza el retorno de nuestro portafolio y al mismo tiempo controla su volatilidad, dado un nivel de riesgo.
En este tutorial aprenderemos como utilizar R para optimizar un portafolio con una estrategia básica y comparar su rendimiento con dos benchmarks (FAANG y el SP&500) utilizando un grupo de acciones aleatorias de las grandes empresas tecnológicas de Estados Unidos con el mismo peso de inversión en un inicio.
Benchmarks (Indices de Comparación)
Para analizar que tan buena fue la optimización de nuestro portafolio (usando datos históricos) se recomienda comparar los retornos observados con alguna referencia. Para esto generalmente se utiliza el S&P500 como benchmark, que es un índice bursátil que mide el rendimiento de las acciones de 500 grandes empresas que cotizan en las bolsas de valores de Estados Unidos.
También, como en este análisis estaremos optimizando un portafolio de empresas del sector tecnológico, resulta conveniente utilizar como referencia el grupo de acciones FAANG compuesto por Facebook (FB), Amazon (AMZN), Apple (APPL), Netflix (NFLX) y Alphabet (GOOG) que en las últimos décadas se han convertido en líderes del sector.
Consulta de la Información Para consultar la información diaria de este conjunto de acciones utilizaremos la función tq_get del paquete tidyquant. Esta función retorna datos relacionados a la acción dado el periodo de búsqueda, en este caso desde el primero de enero del 2018 hasta el 15 de diciembre del 2020, como el precio de apertura, el máximo, el mínimo, el de cierre y uno ajustado. También incluye el volumen transado.
1
2
3
4
#Instalamos los paquetes necesarios
pacman::p_load(xts, zoo, PerformanceAnalytics, quantmod, plotly,
tidyverse, dplyr, PortfolioAnalytics, tidyquant,ROI,
ROI.plugin.quadprog, ROI.plugin.glpk, timetk, ggeasy)
Para nuestro análisis solo necesitaremos el precio ajustado del día, el ticker de la acción y la fecha. A partir de estas variables obtendremos el retorno diario usando tq_transmute. Luego lo convertimos en un objeto XTS.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
##Fecha inicial de nuestro análisis
fecha_inicial <- "2018-01-01"
#Consultamos nuestro primer benchmark S&P 500
xtsSP500_daily_returns <- tq_get("SP500", get = "economic.data",
from = fecha_inicial,to = Sys.Date())%>%
tq_transmute(select = price,
mutate_fun = periodReturn,
period="daily",
type="arithmetic") %>%
select(date,daily.returns) %>%
tk_xts(silent = TRUE)
##Consultamos el Grupo de acciones FAANG y obtenemos los retornos en formato XTS##
FAANG <- c("AAPL", "GOOG", "AMZN", "FB", "NFLX")
xtsFAANG_daily_returns <- FAANG %>%
tq_get(get = "stock.prices",
from = fecha_inicial, to = Sys.Date()) %>%
group_by(symbol) %>%
tq_transmute(select = adjusted,
mutate_fun = periodReturn,
period="daily",
type="arithmetic") %>%
select(symbol, date, daily.returns) %>%
spread(symbol,daily.returns) %>%
tk_xts(silent = TRUE)
Cuando consultamos esta información obtenemos dos objetos xts con los retornos diarios de cada una de las acciones FAANG y del SP500 guardados en xtsFAANG_daily_returns y xtsSP500_daily_returns respectivamente.
Evaluemos que contiene el objeto xtsFAANG_daily_returns.
1
2
3
##Verificamos si se consultaron todas las acciones de nuestro vector #caracter de acciones. Esto es muy importante de validar antes de #proceder
setdiff(FAANG,colnames(xtsFAANG_daily_returns))
View(xtsFAANG_daily_returns)
Para graficar los retornos individuales de las acciones FAANG, convertimos este objeto en un tibble y luego transformamos las columnas a formato largo.
1
2
3
4
5
6
7
8
9
#Hacemos las mencionadas transformaciones para graficar
FAANG_daily_returns <- zoo::fortify.zoo(xtsFAANG_daily_returns)%>%
gather("Symbol","Return", 2:6) %>% rename('Fecha'= Index)
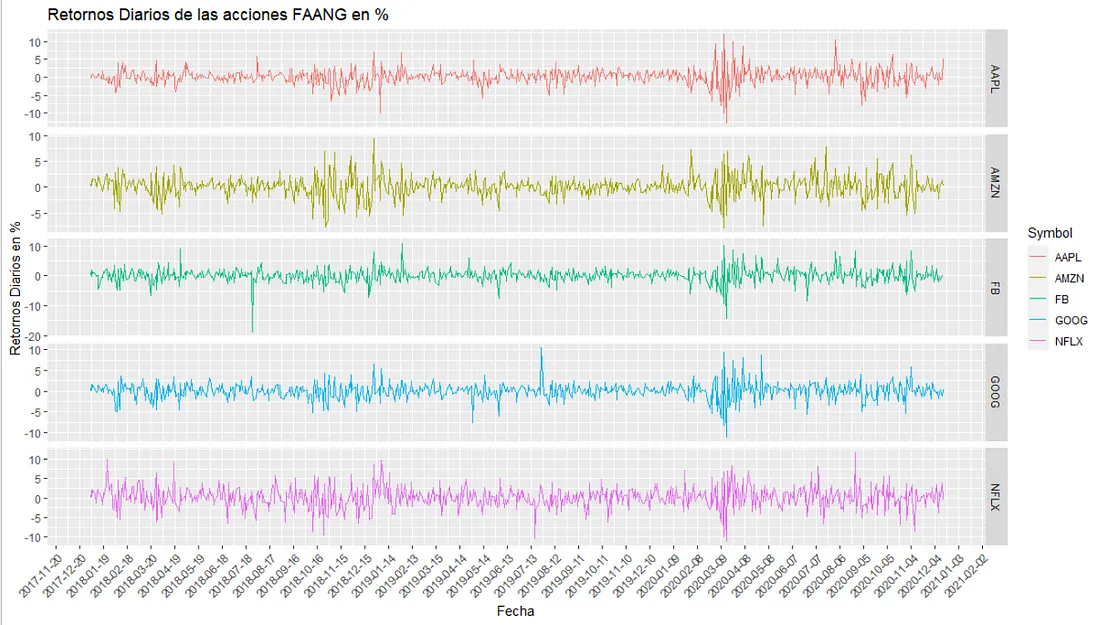
#Graficamos los retornos diarios de cada una de las acciones
qplot(Fecha, Return*100, data = FAANG_daily_returns, geom = "line", group = Symbol, color= Symbol) +
labs(title= "Retornos Diarios de las acciones FAANG en %", y="Retornos Diarios en %") +
facet_grid(Symbol ~ ., scale = "free_y") +
scale_x_date(date_breaks = "30 days") +
easy_rotate_x_labels(angle = 45, side = "right")
Creación del Portafolio FAANG
Luego de consultar los retornos diarios de cada una las acciones FAANG procedemos a crear el portafolio con rebalanceo trimestral con pesos similares para cada acción, es decir la inversión total será dividida equitativamente entre la cantidad de acciones del portafolio, en este caso 20%.
Para este ejercicio nos auxilaremos de la función Return.portfolio del paquete PerformanceAnalytics.
1
2
3
4
5
6
7
8
9
##Creamos los pesos iguales de las acciones FAANG
##Cada acción tendrá un peso inicial correspondiente al 20%
n <- ncol(xtsFAANG_daily_returns)
equal_weights <- rep(1/n, n)
FAANG_EqualWeights <- Return.portfolio(
R= xtsFAANG_daily_returns,
weights= equal_weights,
rebalance_on ="quarters",
verbose= TRUE) ##Activamos el verbose para obtener una lista con #diferentes parámetros relacionados al cálculo del retorno de este #indice
Evolución de los Pesos del Portafolio
Para ver como van evolucionando los pesos del portafolio a través del tiempo, antes de cada rebalanceo trimestral, consultamos el objeto EOP.Weight de la lista creada por Return.portfolio llamada FAANG_EqualWeights y lo guardamos en un dataframe para visualizar.
1
2
3
4
5
6
7
8
9
10
##Graficamos la evolución de los pesos de cada una de las acciones #FAANG para tener una idea de como Return.portfolio hace los #rebalanceos en los periodos especificados
PesosFinalDelPeriodo <- data.frame(FAANG_EqualWeights$EOP.Weight)
##Lo convertimos de un objeto XTS a un tibble para graficar la #evolución de los pesos en el medio de las fechas de rebalanceo
PesosFinalDelPeriodo <-tibble::rownames_to_column(PesosFinalDelPeriodo, "Fecha")
PesosFinalDelPeriodo <- gather(PesosFinalDelPeriodo, Acciones, Pesos, -Fecha)
##Graficamos
PesosFinalDelPeriodo %>%
ggplot( aes(x=as.Date(Fecha), y=Pesos*100, group=Acciones, color= Acciones)) +
geom_line() + ggtitle("Evolución de los Pesos de las Acciones FAANG (Con Rebalanceo Trimestral)") + labs(x= "Fecha", y="Pesos de las Acciones en el Portafolio") +
geom_vline(xintercept = c(seq(as.Date(fecha_inicial), Sys.Date(), by = "quarter")) , linetype="dotted", color = "blue", size=0.3)
Cada línea vertical en el gráfico representa la fecha de rebalanceo del portafolio a la alocación de pesos inicial (20% para cada acción). Esta decisión dependerá de la estrategia de inversión seleccionada alineada a objetivos de corto, mediano o largo plazo. También, el rebalanceo puede ocurrir entre diferentes instrumentos financieros.
Existen otros objetos de la lista creada por Return.portfolio que pueden ser muy útiles para hacer un análisis profundo del portafolio como las contribuciones de cada una de las acciones al retorno general del portafolio.
Contribuciones de las Acciones al Retorno General del Portafolio
Resulta conveniente dar seguimiento a como cada acción contribuye al retorno general del portafolio para determinar si vale la pena mantener la posición o hacer una reevaluación de su peso dentro del portafolio.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
###Sacamos la contribución de cada acción en FAANG al retorno general del portafolio
ContribucionAccion <- data.frame(FAANG_EqualWeights$contribution)
ContribucionAccion <- tibble::rownames_to_column(ContribucionAccion, "Fecha")
ContribucionAccion$Ano <- year(ContribucionAccion$Fecha)
ContribucionAccion$Trimestre <- quarter(ContribucionAccion$Fecha, with_year = TRUE)
##Obtenemos el objeto de los retornos globales del portafolio
Retornos_FAAN_EqualWeights <- as.data.frame(FAANG_EqualWeights$returns)
RetornosFAANG <- tibble::rownames_to_column(Retornos_FAAN_EqualWeights, "Fecha")
##Unimos la contribución y retornos del portafolio
ContribucionyRetornos <- left_join( RetornosFAANG, ContribucionAccion, by="Fecha")
ContribucionyRetornos <- gather(ContribucionyRetornos, Acciones, Pesos, -c(Fecha, Ano, Trimestre))
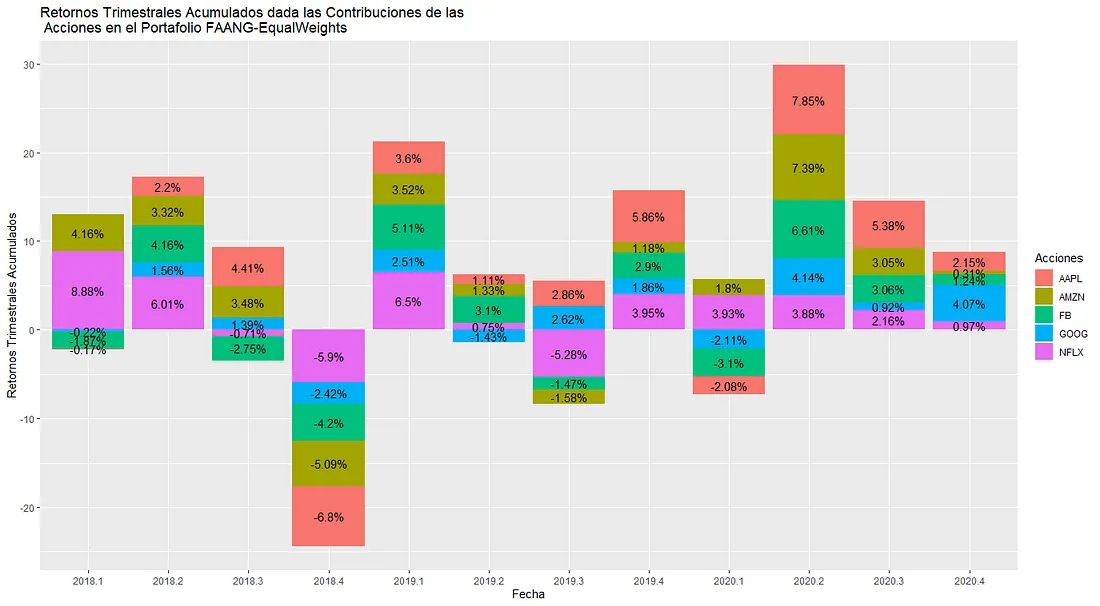
##Contribución Acumulada Trimestral y Grafico
ContribucionAcumuladaTrimestral <- ContribucionyRetornos %>% filter(Acciones!='portfolio.returns') %>% group_by(Acciones, Trimestre) %>% summarise(ContribucionAcumulada= sum(Pesos))
ggplot(ContribucionAcumuladaTrimestral, aes(fill=Acciones, y=ContribucionAcumulada*100, x=as.factor(Trimestre))) +
geom_bar(position="stack", stat="identity")+ ggtitle("Retornos Trimestrales Acumulados dada las Contribuciones de las \n Acciones en el Portafolio FAANG-EqualWeights") +
labs(x= "Fecha", y="Retornos Trimestrales Acumulados") +
geom_text(aes(label= paste0(round(ContribucionAcumulada*100,2), '%')), position=position_stack(0.5), size=4)
1
2
3
4
5
6
7
8
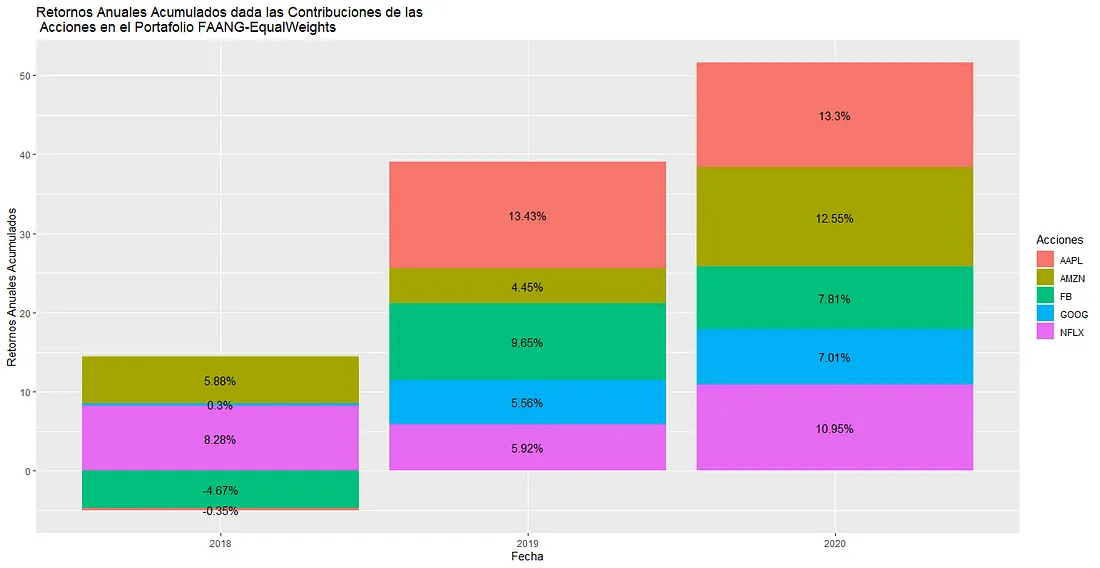
##Contribución Acumulada Anual y Grafico
ContribucionAcumuladaAnual <- ContribucionyRetornos %>% filter(Acciones!='portfolio.returns') %>% group_by(Acciones, Ano) %>% summarise(ContribucionAcumulada= sum(Pesos))
ggplot(ContribucionAcumuladaAnual, aes(fill=Acciones, y=ContribucionAcumulada*100, x=as.factor(Ano))) +
geom_bar(position="stack", stat="identity")+ ggtitle("Retornos Anuales Acumulados dada las Contribuciones de las \n Acciones en el Portafolio FAANG-EqualWeights") +
labs(x= "Fecha", y="Retornos Anuales Acumulados") +
geom_text(aes(label= paste0(round(ContribucionAcumulada*100,2), '%')), position=position_stack(0.5))
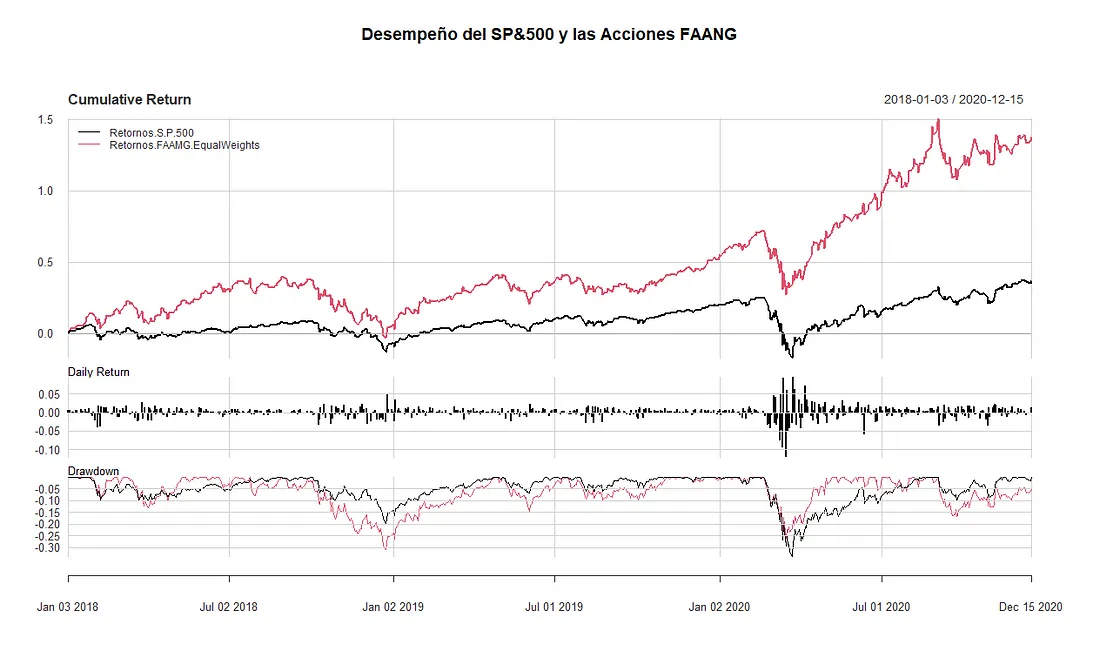
Evaluación del Retorno General del Portafolio
Finalmente, analizamos como se comporta este portafolio en en el periodo analizado y lo comparamos con el S&P 500.
1
2
3
4
5
6
7
8
9
10
##Obtenemos el objeto de retornos del portafolio, para luego ser utilizado en la comparacion
Retornos_FAAN_EqualWeights <- FAANG_EqualWeights$returns
colnames(Retornos_FAAN_EqualWeights) <- "FAAMG-EqualWeights"
##Obtenemos nuestro objeto con los benchmarks obtenidos en la sección anterior para continuar con el análisis
colnames(xtsSP500_daily_returns)[1] <- "Retornos S&P 500"
colnames(Retornos_FAAN_EqualWeights)[1] <- "Retornos FAAMG-EqualWeights"
benchmark_returns <- cbind(xtsSP500_daily_returns, Retornos_FAAN_EqualWeights)
##Graficamos el Rendimiento del portafolio FAANG con el SP&500
charts.PerformanceSummary(benchmark_returns, main= "Desempeño del SP&500 y las Acciones FAANG")
En la próxima entrega de esta serie, veremos como optimizar un portafolio dado un grupo de restricciones y objetivos de minimización de riesgos.